Home  ›  Something That Varies Inversly With Time Spent Reading

Something That Varies Inversly With Time Spent Reading

Written By Wednesday, March 2, 2022 Add Comment Edit

Rational Expressions and Equations

70 Use Direct and Changed Variation

Learning Objectives

By the end of this section, you lot volition be able to:

  • Solve direct variation problems
  • Solve inverse variation bug

When 2 quantities are related past a proportion, we say they are proportional to each other. Another fashion to express this relation is to talk about the variation of the two quantities. Nosotros will talk over direct variation and inverse variation in this section.

Solve Directly Variation Problems

Lindsay gets paid ?15 per hour at her job. If we let s be her bacon and h be the number of hours she has worked, we could model this situation with the equation

s=15h

Lindsay'due south bacon is the production of a constant, fifteen, and the number of hours she works. We say that Lindsay's salary varies direct with the number of hours she works. Two variables vary directly if 1 is the product of a constant and the other.

Direct Variation

For any two variables 10 and y, y varies direct with x if

y=kx,\phantom{\rule{0.2em}{0ex}}\text{where}\phantom{\rule{0.2em}{0ex}}k\ne 0

The constant k is called the constant of variation.

In applications using straight variation, generally we will know values of ane pair of the variables and will be asked to find the equation that relates ten and y. And then we tin use that equation to find values of y for other values of x.

How to Solve Straight Variation Problems

If y varies direct with x and y=20 when x=8, notice the equation that relates x and y.

If y varies directly as x and y=3,\phantom{\rule{0.2em}{0ex}}\text{when}\phantom{\rule{0.2em}{0ex}}x=10. find the equation that relates x and y.

y=\frac{3}{10}x

If y varies direct equally x and y=12\phantom{\rule{0.2em}{0ex}}\text{when}\phantom{\rule{0.2em}{0ex}}x=4 find the equation that relates x and y.

y=3x

We'll list the steps below.

Solve direct variation problems.

  1. Write the formula for straight variation.
  2. Substitute the given values for the variables.
  3. Solve for the constant of variation.
  4. Write the equation that relates ten and y.

At present nosotros'll solve a few applications of direct variation.

When Raoul runs on the treadmill at the gym, the number of calories, c, he burns varies directly with the number of minutes, chiliad, he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.

  1. ⓐ Write the equation that relates c and 1000.
  2. ⓑ How many calories would he burn if he ran on the treadmill for 25 minutes?

The number of calories, c, burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising.

  1. ⓐ Write the equation that relates c and t.
  2. ⓑ How many calories would he burn if he exercises for 90 minutes?

ⓐ c=4.8t ⓑ 432 calories

The distance a moving body travels, d, varies direct with time, t, it moves. A railroad train travels 100 miles in 2 hours

ⓐ Write the equation that relates d and t.
ⓑ How many miles would information technology travel in five hours?

ⓐ d=50t ⓑ 250 miles

In the previous case, the variables c and one thousand were named in the problem. Commonly that is not the case. We will have to name the variables in the next example as part of the solution, just like nosotros exercise in most practical problems.

The number of gallons of gas Eunice's automobile uses varies directly with the number of miles she drives. Last week she drove 469.8 miles and used 14.5 gallons of gas.

  1. ⓐ Write the equation that relates the number of gallons of gas used to the number of miles driven.
  2. ⓑ How many gallons of gas would Eunice's machine apply if she drove 1000 miles?

The distance that Brad travels varies directly with the time spent traveling. Brad travelled 660 miles in 12 hours,

  1. ⓐ Write the equation that relates the number of miles travelled to the time.
  2. ⓑ How many miles could Brad travel in 4 hours?

ⓐ m=55h ⓑ 220 miles

The weight of a liquid varies direct as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.

  1. ⓐ Write the equation that relates the weight to the volume.
  2. ⓑ If a liquid has volume 13 gallons, what is its weight?

ⓐ w=6v ⓑ 78 pounds

In some situations, one variable varies direct with the square of the other variable. When that happens, the equation of direct variation is y=k\phantom{\rule{0.2em}{0ex}}{x}^{2}. We solve these applications but every bit we did the previous ones, by substituting the given values into the equation to solve for grand.

The maximum load a beam will support varies directly with the square of the diagonal of the axle's cross-department. A beam with diagonal iv" will back up a maximum load of 75 pounds.

  1. ⓐ Write the equation that relates the maximum load to the cantankerous-section.
  2. ⓑ What is the maximum load that can be supported past a axle with diagonal viii"?

The distance an object falls is straight proportional to the square of the time it falls. A brawl falls 144 feet in 3 seconds.

ⓐ Write the equation that relates the distance to the time.
ⓑ How far will an object fall in 4 seconds?

ⓐ d=16{t}^{2} ⓑ 256 feet

The area of a circumvolve varies directly every bit the square of the radius. A circular pizza with a radius of half dozen inches has an surface area of 113.04 foursquare inches.

  1. ⓐ Write the equation that relates the area to the radius.
  2. ⓑ What is the area of a pizza with a radius of 9 inches?

ⓐ A=3.14{r}^{2} ⓑ 254.34 square inches

Solve Changed Variation Issues

Many applications involve two variable that vary inversely. As one variable increases, the other decreases. The equation that relates them is y=\frac{k}{x}.

Inverse Variation

For whatsoever two variables x and y, y varies inversely with x if

y=\frac{k}{x},\phantom{\rule{0.2em}{0ex}}\text{where}\phantom{\rule{0.2em}{0ex}}k\ne 0

The constant 1000 is chosen the constant of variation.

The word 'inverse' in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is \frac{1}{x}.

We solve inverse variation problems in the aforementioned way we solved direct variation issues. Simply the general class of the equation has changed. We will copy the procedure box here and just modify 'straight' to 'inverse'.

Solve inverse variation problems.

  1. Write the formula for inverse variation.
  2. Substitute the given values for the variables.
  3. Solve for the constant of variation.
  4. Write the equation that relates 10 and y.

The fuel consumption (mpg) of a automobile varies inversely with its weight. A automobile that weighs 3100 pounds gets 26 mpg on the highway.

  1. ⓐ Write the equation of variation.
  2. ⓑ What would exist the fuel consumption of a car that weighs 4030 pounds?

A car's value varies inversely with its historic period. Elena bought a two-year-old motorcar for ?20,000.

ⓐ Write the equation of variation.
ⓑ What volition exist the value of Elena's motorcar when it is 5 years quondam?

ⓐ v=\frac{40,000}{a} ⓑ ?eight,000

The time required to empty a pool varies inversely equally the rate of pumping. Information technology took Lucy 2.5 hours to empty her pool using a pump that was rated at 400 gpm (gallons per minute).

  1. ⓐ Write the equation of variation.
  2. ⓑ How long will it have her to empty the pool using a pump rated at 500 gpm?

ⓐ t=\frac{1000}{r} ⓑ 2 hours

The frequency of a guitar string varies inversely with its length. A 26" long string has a frequency of 440 vibrations per 2nd.

  1. ⓐ Write the equation of variation.
  2. ⓑ How many vibrations per second will in that location be if the string's length is reduced to twenty" past putting a finger on a fret?

The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a cake of ice melts in 2 hours when the temperature is 65 degrees.

  1. ⓐ Write the equation of variation.
  2. ⓑ How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?

ⓐ h=\frac{130}{t} ⓑ 1\frac{2}{3} hours

The force needed to pause a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-pes long board.

  1. ⓐ Write the equation of variation.
  2. ⓑ How many pounds of pressure is needed to break a 5-foot long board?

ⓐ F=\frac{48}{L} ⓑ ix.six pounds

Section Exercises

Practise Makes Perfect

Solve Direct Variation Problems

In the following exercises, solve.

The corporeality of money Sally earns, P, varies directly with the number, n, of necklaces she sells. When Sally sells 15 necklaces she earns ?150.

  1. ⓐ Write the equation that relates P and n.
  2. ⓑ How much money would she earn if she sold 4 necklaces?

ⓐ P=10n ⓑ \text{?}40

The cost, P, that Eric pays for gas varies directly with the number of gallons, 1000, he buys. It costs him ?l to buy 20 gallons of gas.

  1. ⓐ Write the equation that relates P and grand.
  2. ⓑ How much would 33 gallons cost Eric?

Terri needs to make some pies for a fundraiser. The number of apples, a, varies directly with number of pies, p. It takes ix apples to make two pies.

  1. ⓐ Write the equation that relates a and p.
  2. ⓑ How many apples would Terri demand for six pies?

ⓐ a=4.5p ⓑ 27 apples

Joseph is traveling on a road trip. The altitude, d, he travels before stopping for lunch varies directly with the speed, 5, he travels. He can travel 120 miles at a speed of 60 mph.

  1. ⓐ Write the equation that relates d and v.
  2. ⓑ How far would he travel before stopping for lunch at a rate of 65 mph?

The price of gas that Jesse purchased varies directly to how many gallons he purchased. He purchased 10 gallons of gas for ?39.80.

  1. ⓐ Write the equation that relates the price to the number of gallons.
  2. ⓑ How much will it cost Jesse for 15 gallons of gas?

ⓐ p=3.98g ⓑ \text{?}59.70

The distance that Sarah travels varies directly to how long she drives. She travels 440 miles in 8 hours.

  1. ⓐ Write the equation that relates the distance to the number of hours.
  2. ⓑ How far can Sally travel in 6 hours?

The mass of a liquid varies directly with its book. A liquid with mass 16 kilograms has a volume of 2 liters.

  1. ⓐ Write the equation that relates the mass to the book.
  2. ⓑ What is the volume of this liquid if its mass is 128 kilograms?

ⓐ m=8v ⓑ \text{16 liters}

The length that a jump stretches varies directly with a weight placed at the finish of the spring. When Sarah placed a ten pound watermelon on a hanging calibration, the spring stretched v inches.

  1. ⓐ Write the equation that relates the length of the spring to the weight.
  2. ⓑ What weight of watermelon would stretch the jump half-dozen inches?

The distance an object falls varies directly to the square of the time it falls. A ball falls 45 feet in 3 seconds.

  1. ⓐ Write the equation that relates the distance to the time.
  2. ⓑ How far volition the ball fall in 7 seconds?

ⓐ d=5{t}^{2} ⓑ 245 feet

The maximum load a beam will support varies direct with the foursquare of the diagonal of the beam'southward cross-section. A axle with diagonal 6 inch will support a maximum load of 108 pounds.

  1. ⓐ Write the equation that relates the load to the diagonal of the cross-department.
  2. ⓑ What load volition a axle with a ten inch diagonal support?

The area of a circle varies directly equally the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 foursquare inches.

  1. ⓐ Write the equation that relates the area to the radius.
  2. ⓑ What is the area of a personal pizza with a radius four inches?

ⓐ A=3.14{r}^{2} ⓑ 50.24\phantom{\rule{0.2em}{0ex}}\text{sq. in.}

The distance an object falls varies direct to the square of the time it falls. A ball falls 72 feet in 3 seconds,

  1. ⓐ Write the equation that relates the distance to the time.
  2. ⓑ How far will the ball take fallen in viii seconds?

Solve Inverse Variation Problems

In the following exercises, solve.

Write an changed variation equation to solve the following issues.

The fuel consumption (mpg) of a car varies inversely with its weight. A Toyota Corolla weighs 2800 pounds and gets 33 mpg on the highway.

  1. ⓐ Write the equation that relates the mpg to the car's weight.
  2. ⓑ What would the fuel consumption be for a Toyota Sequoia that weighs 5500 pounds?

ⓐ g=\frac{92,400}{w} ⓑ xvi.8 mpg

A car'south value varies inversely with its age. Jackie bought a 10 year old car for ?two,400.

  1. ⓐ Write the equation that relates the car'due south value to its historic period.
  2. ⓑ What volition exist the value of Jackie's automobile when it is fifteen years quondam ?

The time required to empty a tank varies inversely as the rate of pumping. It took Janet v hours to pump her flooded basement using a pump that was rated at 200 gpm (gallons per infinitesimal),

  1. ⓐ Write the equation that relates the number of hours to the pump charge per unit.
  2. ⓑ How long would it take Janet to pump her basement if she used a pump rated at 400 gpm?

ⓐ t=\frac{1000}{r} ⓑ \text{2.5 hours}

The volume of a gas in a container varies inversely as pressure on the gas. A container of helium has a volume of 370 cubic inches under a pressure of xv psi.

  1. ⓐ Write the equation that relates the volume to the pressure.
  2. ⓑ What would exist the volume of this gas if the pressure was increased to 20 psi?

On a cord musical instrument, the length of a string varies inversely equally the frequency of its vibrations. An xi-inch string on a violin has a frequency of 400 cycles per second.

  1. ⓐ Write the equation that relates the string length to its frequency.
  2. ⓑ What is the frequency of a 10-inch cord?

ⓐ L=\frac{4,400}{f} ⓑ 440 cycles per 2nd

Paul, a dentist, determined that the number of cavities that develops in his patient'southward mouth each year varies inversely to the number of minutes spent brushing each night. His patient, Lori, had 4 cavities when brushing her teeth xxx seconds (0.5 minutes) each night.

  1. ⓐ Write the equation that relates the number of cavities to the fourth dimension spent brushing.
  2. ⓑ How many cavities would Paul expect Lori to have if she had brushed her teeth for two minutes each night?

The number of tickets for a sports fundraiser varies inversely to the price of each ticket. Brianna tin can buy 25 tickets at ?5each.

  1. ⓐ Write the equation that relates the number of tickets to the price of each ticket.
  2. ⓑ How many tickets could Brianna buy if the toll of each ticket was ?two.l?

ⓐ t=\frac{125}{p} ⓑ 50 tickets

Boyle'southward Law states that if the temperature of a gas stays constant, and so the pressure level varies inversely to the volume of the gas. Braydon, a scuba diver, has a tank that holds 6 liters of air under a pressure of 220 psi.

  1. ⓐ Write the equation that relates pressure to volume.
  2. ⓑ If the pressure increases to 330 psi, how much air can Braydon'due south tank hold?

Mixed Practice

The forcefulness needed to intermission a lath varies inversely with its length. If Tom uses 20 pounds of pressure to break a 1.five-foot long board, how many pounds of pressure would he need to use to suspension a half-dozen foot long lath?

\text{5 pounds}

The number of hours it takes for ice to melt varies inversely with the air temperature. A block of ice melts in ii.v hours when the temperature is 54 degrees. How long would it take for the same block of ice to cook if the temperature was 45 degrees?

The length a spring stretches varies directly with a weight placed at the end of the spring. When Meredith placed a six-pound cantaloupe on a hanging calibration, the spring stretched ii inches. How far would the jump stretch if the cantaloupe weighed 9 pounds?

\text{3 inches}

The amount that June gets paid varies directly the number of hours she works. When she worked xv hours, she got paid ?111. How much will she be paid for working xviii hours?

The fuel consumption (mpg) of a car varies inversely with its weight. A Ford Focus weighs 3000 pounds and gets 28.vii mpg on the highway. What would the fuel consumption be for a Ford Expedition that weighs 5,500 pounds? Round to the nearest tenth.

15.6\phantom{\rule{0.2em}{0ex}}\text{mpg}

The book of a gas in a container varies inversely equally the pressure on the gas. If a container of argon has a volume of 336 cubic inches nether a pressure of 2,500 psi, what will be its volume if the force per unit area is decreased to 2,000 psi?

The altitude an object falls varies directly to the square of the fourth dimension it falls. If an object falls 52.8 feet in iv seconds, how far will it fall in 9 seconds?

\text{267.3 feet}

The surface area of the face up of a Ferris cycle varies straight with the square of its radius. If the area of i confront of a Ferris wheel with bore 150 feet is 70,650 foursquare feet, what is the area of one confront of a Ferris wheel with bore of 16 feet?

Everyday Math

Ride Service It costs ?35 for a ride from the metropolis center to the drome, xiv miles away.

  1. ⓐ Write the equation that relates the cost, c, with the number of miles, m.
  2. ⓑ What would it cost to travel 22 miles with this service?

ⓐ c=2.5m ⓑ ?55

Road Trip The number of hours it takes Jack to drive from Boston to Bangor is inversely proportional to his average driving speed. When he drives at an average speed of xl miles per 60 minutes, information technology takes him 6 hours for the trip.

  1. ⓐ Write the equation that relates the number of hours, h, with the speed, southward.
  2. ⓑ How long would the trip take if his average speed was 75 miles per hr?

Writing Exercises

In your own words, explicate the difference between direct variation and inverse variation.

Answers will vary.

Brand upwards an example from your life experience of inverse variation.

Self Check

ⓐ Later on completing the exercises, employ this checklist to evaluate your mastery of the objectives of this department.

This image is four columns and three rows. The first row is the header row. The first header is labeled

ⓑ Subsequently looking at the checklist, do you lot think you lot are well-prepared for the adjacent chapter? Why or why not?

Chapter 8 Review Exercises

Simplify Rational Expressions

Decide the Values for Which a Rational Expression is Undefined

In the following exercises, determine the values for which the rational expression is undefined.

\frac{2a+1}{3a-2}

a\ne \frac{2}{3}

\frac{b-3}{{b}^{2}-16}

\frac{3x{y}^{2}}{5y}

y\ne 0

\frac{u-3}{{u}^{2}-u-30}

Evaluate Rational Expressions

In the post-obit exercises, evaluate the rational expressions for the given values.

\frac{4p-1}{{p}^{2}+5}\phantom{\rule{0.2em}{0ex}}\text{when}\phantom{\rule{0.2em}{0ex}}p=-1

-\frac{5}{6}

\frac{{q}^{2}-5}{q+3}\phantom{\rule{0.2em}{0ex}}\text{when q}=7

\frac{{y}^{2}-8}{{y}^{2}-y-2}\phantom{\rule{0.2em}{0ex}}\text{when}\phantom{\rule{0.2em}{0ex}}y=1

\frac{7}{2}

\frac{{z}^{2}+2}{4z-{z}^{2}}\phantom{\rule{0.2em}{0ex}}\text{when z}=3

Simplify Rational Expressions

In the following exercises, simplify.

\frac{10}{24}

\frac{5}{12}

\frac{8{m}^{4}}{16m{n}^{3}}

\frac{14a-14}{a-1}

14

\frac{{b}^{2}+7b+12}{{b}^{2}+8b+16}

Simplify Rational Expressions with Reverse Factors

In the post-obit exercises, simplify.

\frac{{c}^{2}-c-2}{4-{c}^{2}}

\frac{c+1}{c+2}

\frac{d-16}{16-d}

\frac{7v-35}{25-{v}^{2}}

-\frac{7}{5+v}

\frac{{w}^{2}-3w-28}{49-{w}^{2}}

Add together and Subtract Rational Expressions with a Mutual Denominator

Add together Rational Expressions with a Common Denominator

In the following exercises, add.

\frac{3}{5}+\frac{2}{5}

1

\frac{4{a}^{2}}{2a-1}-\frac{1}{2a-1}

\frac{{p}^{2}+10p}{p+5}+\frac{25}{p+5}

p+5

\frac{3x}{x-1}+\frac{2}{x-1}

Subtract Rational Expressions with a Common Denominator

In the post-obit exercises, subtract.

\frac{{d}^{2}}{d+4}-\frac{3d+28}{d+4}

d+7

\frac{{z}^{2}}{z+10}-\frac{100}{z+10}

\frac{4{q}^{2}-q+3}{{q}^{2}+6q+5}-\frac{3{q}^{2}-q-6}{{q}^{2}+6q+5}

\frac{q-3}{q+5}

\frac{5t+4t+3}{{t}^{2}-25}-\frac{4{t}^{2}-8t-32}{{t}^{2}-25}

Add and Decrease Rational Expressions whose Denominators are Opposites

In the following exercises, add and subtract.

\frac{18w}{6w-1}+\frac{3w-2}{1-6w}

\frac{15w+2}{6w-1}

\frac{{a}^{2}+3a}{{a}^{2}-4}-\frac{3a-8}{4-{a}^{2}}

\frac{2{b}^{2}+3b-15}{{b}^{2}-49}-\frac{{b}^{2}+16b-1}{49-{b}^{2}}

\frac{3b-2}{b+7}

\frac{8{y}^{2}-10y+7}{2y-5}+\frac{2{y}^{2}+7y+2}{5-2y}

Add together and Subtract Rational Expressions With Unlike Denominators

Find the Least Common Denominator of Rational Expressions

In the post-obit exercises, find the LCD.

\frac{4}{{m}^{2}-3m-10},\frac{2m}{{m}^{2}-m-20}

\left(m+2\right)\left(m-5\right)\left(m+4\right)

\frac{6}{{n}^{2}-4},\frac{2n}{{n}^{2}-4n+4}

\frac{5}{3{p}^{2}+17p-6},\frac{2m}{3{p}^{2}-23p-8}

\left(3p+1\right)\left(p+6\right)\left(p+8\right)

Notice Equivalent Rational Expressions

In the following exercises, rewrite every bit equivalent rational expressions with the given denominator.

Rewrite every bit equivalent rational expressions with denominator \left(m+2\right)\left(m-5\right)\left(m+4\right):

\frac{4}{{m}^{2}-3m-10},\frac{2m}{{m}^{2}-m-20}.

Rewrite as equivalent rational expressions with denominator \left(n-2\right)\left(n-2\right)\left(n+2\right):

\frac{6}{{n}^{2}-4n+4},\frac{2n}{{n}^{2}-4}.

Rewrite equally equivalent rational expressions with denominator \left(3p+1\right)\left(p+6\right)\left(p+8\right):

\frac{5}{3{p}^{2}+19p+6},\frac{7p}{3{p}^{2}+25p+8}

Add Rational Expressions with Different Denominators

In the following exercises, add.

\frac{2}{3}+\frac{3}{5}

\frac{19}{15}

\frac{7}{5a}+\frac{3}{2b}

\frac{2}{c-2}+\frac{9}{c+3}

\frac{11c-12}{\left(c-2\right)\left(c+3\right)}

\frac{3d}{{d}^{2}-9}+\frac{5}{{d}^{2}+6d+9}

\frac{2x}{{x}^{2}+10x+24}+\frac{3x}{{x}^{2}+8x+16}

\frac{5{x}^{2}+26x}{\left(x+4\right)\left(x+4\right)\left(x+6\right)}

\frac{5q}{{p}^{2}q-{p}^{2}}+\frac{4q}{{q}^{2}-1}

Decrease Rational Expressions with Different Denominators

In the post-obit exercises, subtract and add.

\frac{3v}{v+2}-\frac{v+2}{v+8}

\frac{2\left({v}^{2}+10v-2\right)}{\left(v+2\right)\left(v+8\right)}

\frac{-3w-15}{{w}^{2}+w-20}-\frac{w+2}{4-w}

\frac{7m+3}{m+2}-5

\frac{2m-7}{m+2}

\frac{n}{n+3}+\frac{2}{n-3}-\frac{n-9}{{n}^{2}-9}

\frac{8d}{{d}^{2}-64}-\frac{4}{d+8}

\frac{4}{d-8}

\frac{5}{12{x}^{2}y}+\frac{7}{20x{y}^{3}}

Simplify Circuitous Rational Expressions

Simplify a Complex Rational Expression by Writing it as Division

In the following exercises, simplify.

\frac{\frac{5a}{a+2}}{\frac{10{a}^{2}}{{a}^{2}-4}}

\frac{a-2}{2a}

\frac{\frac{2}{5}+\frac{5}{6}}{\frac{1}{3}+\frac{1}{4}}

\frac{x-\frac{3x}{x+5}}{\frac{1}{x+5}+\frac{1}{x-5}}

\frac{\left(x-8\right)\left(x-5\right)}{2}

\frac{\frac{2}{m}+\frac{m}{n}}{\frac{n}{m}-\frac{1}{n}}

Simplify a Circuitous Rational Expression past Using the LCD

In the post-obit exercises, simplify.

\frac{6+\frac{2}{q-4}}{\frac{5}{q+4}}

\frac{\left(q-2\right)\left(q+4\right)}{5\left(q-4\right)}

\frac{\frac{3}{{a}^{2}}-\frac{1}{b}}{\frac{1}{a}+\frac{1}{{b}^{2}}}

\frac{\frac{2}{{z}^{2}-49}+\frac{1}{z+7}}{\frac{9}{z+7}+\frac{12}{z-7}}

\frac{z-5}{23z+21}

\frac{\frac{3}{{y}^{2}-4y-32}}{\frac{2}{y-8}+\frac{1}{y+4}}

Solve Rational Equations

Solve Rational Equations

In the following exercises, solve.

\frac{1}{2}+\frac{2}{3}=\frac{1}{x}

\frac{6}{7}

1-\frac{2}{m}=\frac{8}{{m}^{2}}

\frac{1}{b-2}+\frac{1}{b+2}=\frac{3}{{b}^{2}-4}

\frac{3}{2}

\frac{3}{q+8}-\frac{2}{q-2}=1

\frac{v-15}{{v}^{2}-9v+18}=\frac{4}{v-3}+\frac{2}{v-6}

\text{no solution}

\frac{z}{12}+\frac{z+3}{3z}=\frac{1}{z}

Solve a Rational Equation for a Specific Variable

In the following exercises, solve for the indicated variable.

\frac{V}{l}=hw\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}l

l=\frac{V}{hw}

\frac{1}{x}-\frac{2}{y}=5\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}y

x=\frac{y+5}{z-7}\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}z

z=\frac{y+5+7x}{x}

P=\frac{k}{V}\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}V

Solve Proportion and Similar Figure Applications Similarity

Solve Proportions

In the following exercises, solve.

\frac{x}{4}=\frac{3}{5}

\frac{12}{5}

\frac{3}{y}=\frac{9}{5}

\frac{s}{s+20}=\frac{3}{7}

15

\frac{t-3}{5}=\frac{t+2}{9}

In the following exercises, solve using proportions.

Rachael had a 21 ounce strawberry shake that has 739 calories. How many calories are there in a 32 ounce shake?

1161\phantom{\rule{0.2em}{0ex}}\text{calories}

Leo went to Mexico over Christmas break and changed ?525 dollars into Mexican pesos. At that time, the exchange charge per unit had ?1 Us is equal to xvi.25 Mexican pesos. How many Mexican pesos did he get for his trip?

Solve Similar Effigy Applications

In the following exercises, solve.

∆ABC is similar to ∆XYZ. The lengths of two sides of each triangle are given in the effigy. Find the lengths of the 3rd sides.

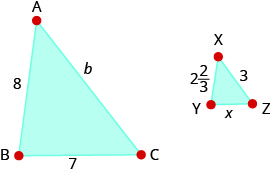
This image shows two triangles. The large triangle is labeled A B C. The length from A to B is labeled 8. The length from B to C is labeled 7. The length from C to A is labeled b. The smaller triangle is triangle x y z. The length from x to y is labeled 2 and two-thirds. The length from y to z is labeled x. The length from x to z is labeled 3.

b=9;x=2\frac{1}{3}

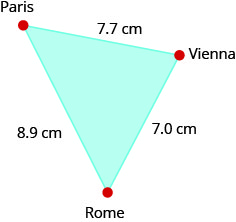
On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the effigy beneath. If the bodily distance from Rome to Vienna is 700 miles, find the altitude from

  1. ⓐ Paris to Rome
  2. ⓑ Paris to Vienna

This is an image of a triangle. Clockwise beginning at the top, each vertex is labeled. The top vertex is labeled

Tony is 5.75 feet tall. Late ane afternoon, his shadow was 8 feet long. At the same time, the shadow of a nearby tree was 32 feet long. Observe the tiptop of the tree.

23 feet

The tiptop of a lighthouse in Pensacola, Florida is 150 feet. Standing next to the statue, 5.5 foot alpine Natalie bandage a 1.ane human foot shadow How long would the shadow of the lighthouse exist?

Solve Uniform Motility and Piece of work Applications Bug

Solve Compatible Motion Applications

In the following exercises, solve.

When making the 5-hour bulldoze home from visiting her parents, Lisa ran into bad weather. She was able to bulldoze 176 miles while the weather was good, only then driving 10 mph slower, went 81 miles in the bad weather. How fast did she bulldoze when the weather was bad?

\text{45 mph}

Mark is riding on a plane that tin can fly 490 miles with a tailwind of xx mph in the same fourth dimension that it tin can fly 350 miles against a tailwind of 20 mph. What is the speed of the aeroplane?

John can ride his bicycle eight mph faster than Luke can ride his wheel. It takes Luke 3 hours longer than John to ride 48 miles. How fast can John ride his bike?

\text{16 mph}

Marking was training for a triathlon. He ran eight kilometers and biked 32 kilometers in a total of 3 hours. His running speed was eight kilometers per hour less than his biking speed. What was his running speed?

Solve Work Applications

In the following exercises, solve.

Jerry can frame a room in i hour, while Jake takes iv hours. How long could they frame a room working together?

\frac{4}{5}\phantom{\rule{0.2em}{0ex}}\text{hour}

Lisa takes three hours to mow the lawn while her cousin, Barb, takes 2 hours. How long will it accept them working together?

Jeffrey tin paint a house in 6 days, but if he gets a helper he can practise it in 4 days. How long would it take the helper to paint the house alone?

12\phantom{\rule{0.2em}{0ex}}\text{days}

Sue and Deb work together writing a book that takes them xc days. If Sue worked alone it would accept her 120 days. How long would information technology take Deb to write the book alone?

Use Directly and Inverse Variation

Solve Straight Variation Problems

In the following exercises, solve.

Vanessa is traveling to encounter her fiancé. The altitude, d, varies directly with the speed, v, she drives. If she travels 258 miles driving 60 mph, how far would she travel going lxx mph?

If the cost of a pizza varies directly with its bore, and if an 8" diameter pizza costs ?12, how much would a six" diameter pizza price?

\text{?}9

The distance to cease a car varies directly with the foursquare of its speed. Information technology takes 200 anxiety to terminate a car going fifty mph. How many feet would information technology accept to cease a automobile going 60 mph?

Solve Inverse Variation Issues

In the following exercises, solve.

The number of tickets for a music fundraiser varies inversely with the toll of the tickets. If Madelyn has just enough money to purchase 12 tickets for ?6, how many tickets can Madelyn afford to buy if the price increased to ?eight?

97\phantom{\rule{0.2em}{0ex}}\text{tickets}

On a string musical instrument, the length of a string varies inversely with the frequency of its vibrations. If an 11-inch string on a violin has a frequency of 360 cycles per 2d, what frequency does a 12 inch string take?

Practice Test

In the following exercises, simplify.

\frac{3{a}^{2}b}{6a{b}^{2}}

\frac{a}{2b}

\frac{5b-25}{{b}^{2}-25}

In the following exercises, perform the indicated operation and simplify.

\frac{4x}{x+2}·\frac{{x}^{2}+5x+6}{12{x}^{2}}

\frac{x+3}{3x}

\frac{5y}{4y-8}·\frac{{y}^{2}-4}{10}

\frac{4}{pq}+\frac{5}{p}

\frac{4+5q}{pq}

\frac{1}{z-9}-\frac{3}{z+9}

\frac{\frac{2}{3}+\frac{3}{5}}{\frac{2}{5}}

\frac{19}{16}

\frac{\frac{1}{m}-\frac{1}{n}}{\frac{1}{n}+\frac{1}{m}}

In the following exercises, solve each equation.

\frac{1}{2}+\frac{2}{7}=\frac{1}{x}

\frac{14}{11}

\frac{5}{y-6}=\frac{3}{y+6}

\frac{1}{z-5}+\frac{1}{z+5}=\frac{1}{{z}^{2}-25}

\frac{1}{2}

\frac{t}{4}=\frac{3}{5}

\frac{2}{r-2}=\frac{3}{r-1}

four

In the following exercises, solve.

The recommended erythromycin dosage for dogs, is 5 mg for every pound the dog weighs. If Daisy weighs 25 pounds, how many milligrams of erythromycin should her veterinarian prescribe?

125\phantom{\rule{0.2em}{0ex}}\text{mg}

Julia spent four hours Lord's day afternoon exercising at the gym. She ran on the treadmill for 10 miles and then biked for 20 miles. Her biking speed was 5 mph faster than her running speed on the treadmill. What was her running speed?

Kurt tin can ride his bike for 30 miles with the wind in the same amount of time that he can go 21 miles against the wind. If the wind's speed is 6 mph, what is Kurt's speed on his bike?

\text{14 mph}

Amanda jogs to the park 8 miles using one road and and so returns via a 14-mile road. The render trip takes her one 60 minutes longer than her jog to the park. Find her jogging rate.

An experienced window washer can wash all the windows in Mike's house in 2 hours, while a new trainee tin can launder all the windows in seven hours. How long would it take them working together?

1\frac{5}{9}\phantom{\rule{0.2em}{0ex}}\text{hours}

Josh can divide a truckload of logs in 8 hours, but working with his dad they can go it done in 3 hours. How long would it accept Josh'south dad working solitary to split the logs?

The price that Tyler pays for gas varies straight with the number of gallons he buys. If 24 gallons cost him ?59.76, what would 30 gallons cost?

\text{?}74.70

The book of a gas in a container varies inversely with the pressure on the gas. If a container of nitrogen has a book of 29.5 liters with 2000 psi, what is the volume if the tank has a 14.vii psi rating? Circular to the nearest whole number.

The cities of Dayton, Columbus, and Cincinnati form a triangle in southern Ohio, every bit shown on the effigy below, that gives the map distances between these cities in inches.

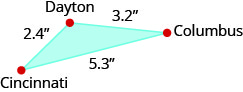
This is an image of a triangle. Clockwise beginning at the top, each vertex is labeled. The top vertex is labeled

The actual distance from Dayton to Cincinnati is 48 miles. What is the actual altitude betwixt Dayton and Columbus?

64 miles

taylordepud1998.blogspot.com

Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/use-direct-and-inverse-variation/

0 Response to "Something That Varies Inversly With Time Spent Reading"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel